Skip to main content
SpringerLink
Log in

Direct Discretization Method for the Cahn–Hilliard Equation on an Evolving Surface

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

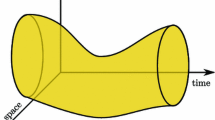
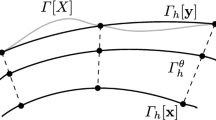
We propose a simple and efficient direct discretization scheme for solving the Cahn–Hilliard (CH) equation on an evolving surface. By using a conservation law and transport formulae, we derive the CH equation on evolving surfaces. An evolving surface is discretized using an unstructured triangular mesh. The discrete CH equation is defined on the surface mesh and its dual surface polygonal tessellation. The evolving triangular surfaces are then realized by moving the surface nodes according to a given velocity field. The proposed scheme is based on the Crank–Nicolson scheme and a linearly stabilized splitting scheme. The scheme is second-order accurate, with respect to both space and time. The resulting system of discrete equations is easy to implement, and is solved by using an efficient biconjugate gradient stabilized method. Several numerical experiments are presented to demonstrate the performance and effectiveness of the proposed numerical scheme.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  1. Cahn, J.W., Hilliard, J.E.: Free energy of a non-uniform system I. Interfacial free energy. J. Chem. Phys. 28, 258–267 (1958)

    Article  Google Scholar 

  2. Armstrong, N.J., Painter, K.J., Sherratt, J.A.: A continuum approach to modelling cell–cell adhesion. J. Theor. Biol. 243, 98–113 (2006)

    Article  MathSciNet  Google Scholar 

  3. Wise, S., Lowengrub, J., Frieboes, H., Cristini, V.: Three-dimensional multispecies nonlinear tumor growth: I. model and numerical method. J. Theor. Biol. 253, 524–543 (2008)

    Article  MathSciNet  Google Scholar 

  4. Kim, J.: Phase-field models for multi-component fluid flows. Commun. Comput. Phys. 12, 613–661 (2012)

    Article  MathSciNet  Google Scholar 

  5. Li, Y., Choi, J.-I., Kim, J.: A phase-field fluid modeling and computation with interfacial profile correction term. Commun. Nonlinear Sci. Numer. Simul. 30, 84–100 (2016)

    Article  MathSciNet  Google Scholar 

  6. Li, Y., Shin, J., Choi, Y., Kim, J.S.: Three-dimensional volume reconstruction from slice data using phase-field models. Comput. Vis. Image Und. 137, 115–124 (2015)

    Article  Google Scholar 

  7. Archer, A.J., Evans, R.: Dynamical density functional theory and its application to spinodal decomposition. J. Chem. Phys. 121, 4246–4254 (2004)

    Article  Google Scholar 

  8. Marconi, U.M.B., Tarazona, P.: Dynamic density functional theory of fluids. J. Chem. Phys. 110, 8032–8044 (1999)

    Article  Google Scholar 

  9. Yang, S.-D., Lee, H.G., Kim, J.S.: A phase-field approach for minimizing the area of triply periodic surfaces with volume constraint. Comput. Phys. Commun. 181, 1037–1046 (2010)

    Article  MathSciNet  Google Scholar 

  10. Erlebacher, J., Aziz, M.J., Karma, A., Dimitrov, N., Sieradzki, K.: Evolution of nanoporosity in dealloying. Nature 410, 450–453 (2001)

    Article  Google Scholar 

  11. Baumgart, T., Hess, S., Webb, W.: Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature 425, 821–824 (2003)

    Article  Google Scholar 

  12. Tang, P., Qiu, F., Zhang, H., Yang, Y.: Phase separation patterns for diblock copolymers on spherical surfaces: a finite volume method. Phys. Rev. E 72, 016710 (2005)

    Article  Google Scholar 

  13. Jeong, D., Kim, J.K.: Microphase separation patterns in diblock copolymers on curved surfaces using a nonlocal Cahn-Hilliard equation. Eur. Phys. J. E 38, 1–7 (2015)

    Article  Google Scholar 

  14. Bausch, A., et al.: Grain boundary scars and spherical crystallography. Science 299, 1716–1718 (2003)

    Article  Google Scholar 

  15. Lee, H.-G., Kim, J.: A simple and efficient finite difference method for the phase-field crystal equation on curved surfaces. Comput. Methods Appl. Mech. Eng. 307, 32–43 (2016)

    Article  MathSciNet  Google Scholar 

  16. Mercker, M., Ptashnyk, M., Kuhnle, J., Hartmann, D., Weiss, M., Jager, W.: A multiscale approach to curvature modulated sorting in biological membranes. J. Theor. Biol. 301, 67–82 (2012)

    Article  MathSciNet  Google Scholar 

  17. He, Y., Liu, Y., Tang, T.: On large time-stepping methods for the Cahn–Hilliard equation. Appl. Numer. Math. 57, 616–628 (2007)

    Article  MathSciNet  Google Scholar 

  18. Gomez, H., Hughes, T.J.R.: Provably unconditionally stable, second-order time-accurate, mixed variational methods for phase-field models. J. Comput. Phys. 230, 5310–5327 (2011)

    Article  MathSciNet  Google Scholar 

  19. Li, Y., Jeong, D., Shin, J., Kim, J.S.: A conservative numerical method for the Cahn–Hilliard equation with Dirichlet boundary conditions in complex domains. Comput. Math. Appl. 65, 102–115 (2013)

    Article  MathSciNet  Google Scholar 

  20. Li, Y., Lee, H.G., Xia, B., Kim, J.: A compact fourth-order finite difference scheme for the three-dimensional Cahn–Hilliard equation. Comput. Phys. Commun. 200, 108–116 (2016)

    Article  MathSciNet  Google Scholar 

  21. Song, H., Shu, C.-W.: Unconditional energy stability analysis of a second order implicit-explicit local discontinuous galerkin method for the Cahn–Hilliard equation. 1–26 (2017)

  22. Du, Q., Ju, L., Tian, L.: Finite element approximation of the Cahn–Hilliard equation on surfaces. Comput. Methods Appl. Mech. Eng. 200, 2458–2470 (2011)

    Article  MathSciNet  Google Scholar 

  23. Elliott, C.M., Ranner, T.: Evolving surface finite element method for the Cahn–Hilliard equation. Numer. Math. 129, 483–534 (2015)

    Article  MathSciNet  Google Scholar 

  24. Rätz, A., Voigt, A.: PDE’s on surfaces—A diffuse interface approach. Commun. Math. Sci. 4, 575–590 (2006)

    Article  MathSciNet  Google Scholar 

  25. Witkowski, T., Backofena, R., Voigt, A.: The influence of membrane bound proteins on phase separation and coarsening in cell membranes. Phys. Chem. Chem. Phys. 14, 14509–14515 (2012)

    Article  Google Scholar 

  26. Bertalmio, M., Cheng, L.-T., Osher, S., Sapiro, G.: Variational problems and partial differential equations on implicit surfaces. J. Comput. Phys. 174, 759–780 (2001)

    Article  MathSciNet  Google Scholar 

  27. Xu, J.-J., Zhao, H.-K.: An Eulerian formulation for solving partial differential equations along a moving interface. J. Sci. Comput. 19, 1–3 (2003)

    Article  MathSciNet  Google Scholar 

  28. Adalsteinsson, D., Sethian, J.A.: Transport and diffusion of material quantities on propagating interfaces via level set methods. J. Comput. Phys. 185, 271–288 (2003)

    Article  MathSciNet  Google Scholar 

  29. Greer, J., Bertozzi, A.L., Saporo, G.: Fourth order partial differential equations on general geometries. J. Comput. Phys. 216, 216–246 (2006)

    Article  MathSciNet  Google Scholar 

  30. Dziuk, G., Elliott, C.M.: An Eulerian approach to transport and diffusion on evolving implicit surfaces. Comput. Vis. Sci. 13, 17–28 (2010)

    Article  MathSciNet  Google Scholar 

  31. Leung, S., Lowengrub, J., Zhao, H.K.: A grid based particle method for solving partial differential equations on evolving surfaces and modeling high order geometrical motion. J. Comput. Phys. 230, 2540–2561 (2011)

    Article  MathSciNet  Google Scholar 

  32. Rong, G., Jin, M., Shuai, L., Guo, X.: Centroidal Voronoi tessellation in universal covering space of manifold surfaces. Comp. Aided Geom. Des. 28, 475–496 (2011)

    Article  MathSciNet  Google Scholar 

  33. Sun, F., Choi, Y.-K., Wang, W., Yan, D.-M., Liu, Y., Lévy, B.: Obtuse triangle suppression in anisotropic meshes. Comp. Aided Geom. Des. 28, 537–548 (2011)

    Article  MathSciNet  Google Scholar 

  34. Dziuk, G., Elliott, C.M.: Finite elements on evolving surfaces. IMA J. Numer. Anal. 27, 262–292 (2007)

    Article  MathSciNet  Google Scholar 

  35. Willmore, T.J.: Riemannian Geometry. Clarendon Press, New York (1993)

    MATH  Google Scholar 

  36. Chen, S.-G., Wu, J.-Y.: Estimating normal vectors and curvatures by centroid weights. Comp. Aided Geom. Des. 21, 447–458 (2004)

    Article  MathSciNet  Google Scholar 

  37. Chen, S.-G., Wu, J.: Discrete conservation laws on evolving surfaces. SIAM J. Sci. Comput. 38, A1725–A1742 (2016)

    Article  MathSciNet  Google Scholar 

  38. Chen, S.-G., Wu, J.: Discrete conservation laws on curved surfaces. SIAM J. Sci. Comput. 36, 719–39 (2013)

    Article  MathSciNet  Google Scholar 

  39. Li, Y., Wang, N., Kim, J.: An unconditionally energy-stable second-order time-accurate scheme for the Cahn-Hilliard equation on surfaces. Commun. Nonlinear. Sci. Numer. Simul. 53, 213–227 (2017)

    Article  MathSciNet  Google Scholar 

  40. van der Vorst, H.A.: BI-CGSTAB: a fast and smoothly converging variant of BI-CG for the solution of nonsymmetriclinear systems. SIAM J. Sci. Stat. Comput. 13(2), 631–644 (1992)

    Article  Google Scholar 

  41. Hua, H., Li, Y., Shin, J., Song, H., Kim, J.: Effect of confinement on droplet deformation in shear flow. Int. J. Comput. Fluid D. 27, 317–331 (2013)

    Article  Google Scholar 

  42. Li, Y., Kim, J.: Three-dimensional simulations of the cell growth and cytokinesis using the immersed boundary method. Math. Biosci. 271, 118–127 (2016)

    Article  MathSciNet  Google Scholar 

  43. Li, Y., Kim, J.: Multiphase image segmentation using a phase-field model. Comput. Math. Appl. 62, 737–745 (2011)

    Article  MathSciNet  Google Scholar 

  44. Li, Y., Jeong, D., Choi, J.-I., Lee, S., Kim, J.: Fast local image inpainting based on the Allen–Cahn model. Digit. Signal Process. 37, 65–74 (2015)

    Article  Google Scholar 

  45. Li, Y., Kim, J.: Fast and efficient narrow volume reconstruction from scattered data. Pattern Recognit. 48, 4057–4069 (2015)

    Article  Google Scholar 

  46. Li, Y., Yun, A., Kim, J.: An immersed boundary method for simulating a single axisymmetric cell growth and division. J. Math. Biol. 65, 653–675 (2012)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

Y.B. Li is supported by National Natural Science Foundation of China(Nos. 11601416, 11631012). The corresponding author (J.S. Kim) was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A1B03933243). The authors thank the reviewers for the constructive and helpful comments concerning the revision of this article.

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, 710049, China

    Yibao Li & Xuelin Qi

  2. Department of Mathematics, Korea University, Seoul, 136-701, Republic of Korea

    Junseok Kim

Authors
  1. Yibao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xuelin Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Junseok Kim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Junseok Kim.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Y., Qi, X. & Kim, J. Direct Discretization Method for the Cahn–Hilliard Equation on an Evolving Surface. J Sci Comput 77, 1147–1163 (2018). https://doi.org/10.1007/s10915-018-0742-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10915-018-0742-6

Keywords

Search

Navigation